Experiments

V22: Intrinsic Predictive Gradient

V22: Intrinsic Predictive Gradient

Period: 2026-02-19. Substrate: V21 + within-lifetime gradient descent on energy prediction.

The key mechanism: Each environment step, the agent predicts its own energy delta, observes the truth, and updates its phenotype via SGD. The computational equivalent of the free energy principle: minimize surprise about your own persistence. No external reward, no human labels.

loss=(ΔE^−ΔEactual)2⇒phenotype−=lr⋅∇loss\text{loss} = (\hat{\Delta E} - \Delta E_{\text{actual}})^2 \quad \Rightarrow \quad \text{phenotype} \mathrel{-}= \text{lr} \cdot \nabla \text{loss}
MetricSeed 42Seed 123Seed 7Mean
Mean robustness0.9650.9900.9880.981
Mean Φ\intinfo0.1060.1000.0850.097
Mean pred MSE6.4e-41.1e-44.0e-43.8e-4
Final LR0.004830.005290.004370.00483

Within-lifetime learning is unambiguously working (100-15000x MSE improvement per lifetime, 3/3 seeds). LR not suppressed — evolution maintains learning. But robustness not improved over V20.

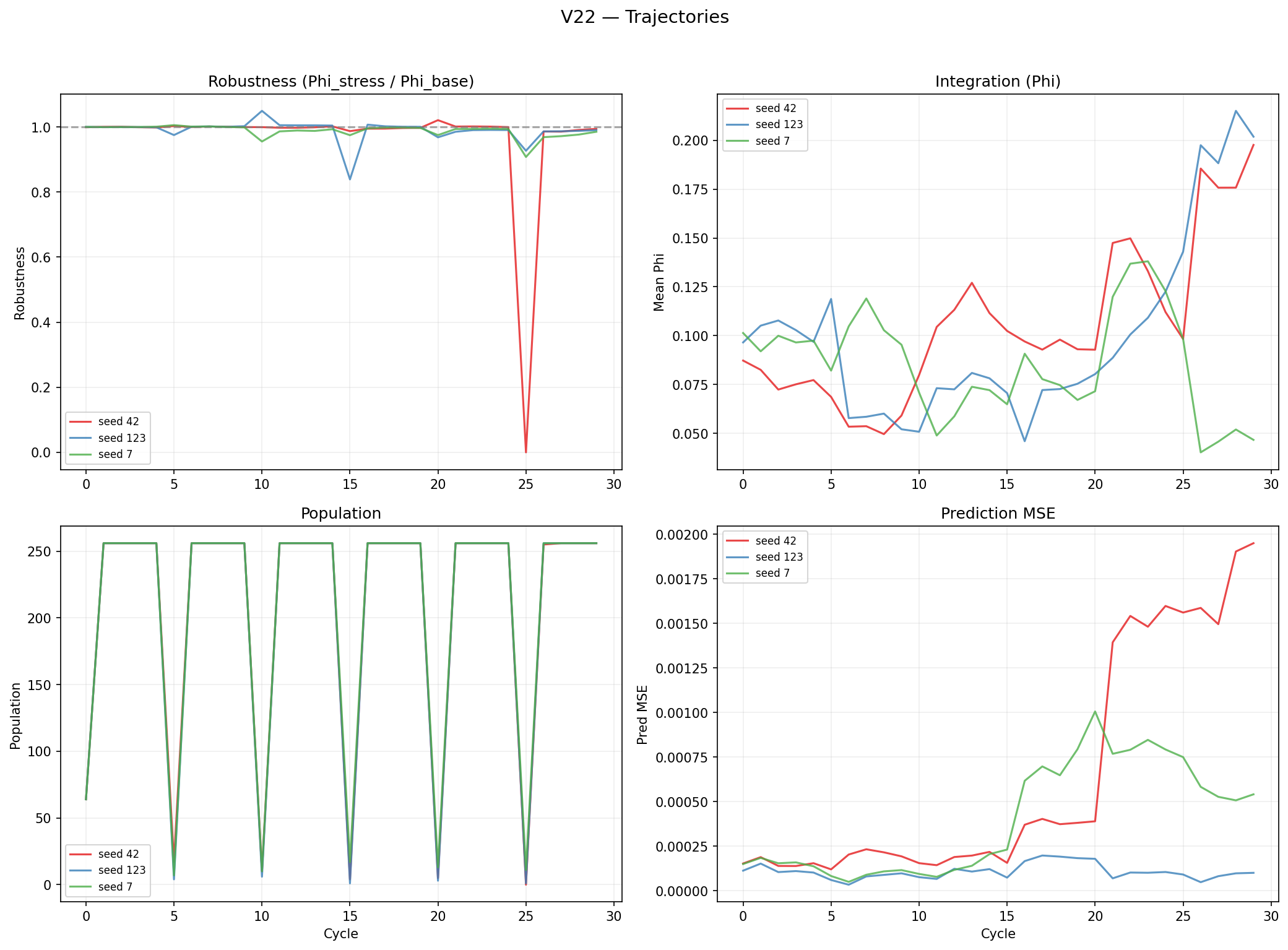
V22 trajectories: robustness, integration, population, and prediction MSE
V22 evolution trajectories. Top-left: robustness stays near 1.0 between droughts, drops sharply during them. Top-right: mean Φ ranges 0.05–0.20 — moderate integration that doesn't trend upward. Bottom-left: population dynamics with regular drought dips. Bottom-right: prediction MSE stays low (10⁻⁴ scale) — the gradient works, but better prediction doesn't translate to higher integration.
V22 agent evolution filmstrip showing grid state across cycles
V22 agent evolution (seed 42). Grid snapshots across evolution cycles C0–C29. Agents (colored dots) on a resource landscape (green). Population oscillates with drought cycles. The visual shows the substrate is working — agents persist, reproduce, and die in response to resource dynamics — but the spatial patterns alone don't reveal the internal integration story.

Prediction ≠ integration. The gradient makes agents better individual forecasters without creating cross-component coordination. A single linear prediction head can be satisfied by a subset of hidden units — no cross-component coupling required. This is the decomposability problem: linear readouts are always factored.

Source code